Contents

Summary statistics

Overview of three examples of how summary statistics can hide differences that are exposed through visualisation

The three sources are:

See also (not considered here): https://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.1002128

import pandas as pd

from IPython.display import display_html
from itertools import chain,cycle

import numpy as np
import matplotlib.pyplot as plt

Anscombe (1973)

# define file locations

path = '/Users/aidanair/Documents/DATA/ALL_DATASETS/anscombe_csvs/'

file1 = 'ans1.csv'
file2 = 'ans2.csv'
file3 = 'ans3.csv'
file4 = 'ans4.csv'

# read in and assign to four different variables

one = pd.read_csv(path + file1)
two = pd.read_csv(path + file2)
three = pd.read_csv(path + file3)
four = pd.read_csv(path + file4)

# VERY HELPFUL FUNCTION TAKEN FROM THIS STACK OVERFLOW USER TO DISPLAY DATAFRAMES SIDE BY SIDE
# https://stackoverflow.com/questions/38783027/jupyter-notebook-display-two-pandas-tables-side-by-side

def display_side_by_side(*args, titles=cycle([''])):
    html_str=''
    
    for df,title in zip(args, chain(titles,cycle(['</br>'])) ):
        html_str+='<th style="text-align:center"><td style="vertical-align:top">'
        html_str+=f'<h2>{title}</h2>'
        html_str+=df.to_html().replace('table','table style="display:inline"')
        html_str+='</td></th>'
        
    display_html(html_str,raw=True)

# run function: show data in the four dfs

display_side_by_side(one, two, three, four, titles=['one','two', 'three', 'four'])

one

x1 y1
0 10 8.04
1 8 6.95
2 13 7.58
3 9 8.81
4 11 8.33
5 14 9.96
6 6 7.24
7 4 4.26
8 12 10.84
9 7 4.82
10 5 5.68

two

x2 y2
0 10 9.14
1 8 8.14
2 13 8.74
3 9 8.77
4 11 9.26
5 14 8.10
6 6 6.13
7 4 3.10
8 12 9.13
9 7 7.26
10 5 4.74

three

x3 y3
0 10 7.46
1 8 6.77
2 13 12.74
3 9 7.11
4 11 7.81
5 14 8.84
6 6 6.08
7 4 5.39
8 12 8.15
9 7 6.42
10 5 5.73

four

x4 y4
0 8 6.58
1 8 5.76
2 8 7.71
3 8 8.84
4 8 8.47
5 8 7.04
6 8 5.25
7 19 12.50
8 8 5.56
9 8 7.91
10 8 6.89 
# show summary statistics (function will run with added methods chained on)

display_side_by_side(one.describe().round(2), 
                     two.describe().round(2), 
                     three.describe().round(2), 
                     four.describe().round(2), 
                     titles=['one','two', 'three', 'four'])

one

x1 y1
count 11.00 11.00
mean 9.00 7.50
std 3.32 2.03
min 4.00 4.26
25% 6.50 6.32
50% 9.00 7.58
75% 11.50 8.57
max 14.00 10.84

two

x2 y2
count 11.00 11.00
mean 9.00 7.50
std 3.32 2.03
min 4.00 3.10
25% 6.50 6.70
50% 9.00 8.14
75% 11.50 8.95
max 14.00 9.26

three

x3 y3
count 11.00 11.00
mean 9.00 7.50
std 3.32 2.03
min 4.00 5.39
25% 6.50 6.25
50% 9.00 7.11
75% 11.50 7.98
max 14.00 12.74

four

x4 y4
count 11.00 11.00
mean 9.00 7.50
std 3.32 2.03
min 8.00 5.25
25% 8.00 6.17
50% 8.00 7.04
75% 8.00 8.19
max 19.00 12.50 
# what about correlation between x and y in the four datasets? The same up to three decimal points

print(np.corrcoef(one.x1, one.y1)[1][0].round(5))
print(np.corrcoef(two.x2, two.y2)[1][0].round(5))
print(np.corrcoef(three.x3, three.y3)[1][0].round(5))
print(np.corrcoef(four.x4, four.y4)[1][0].round(5))

0.81642
0.81624
0.81629
0.81652

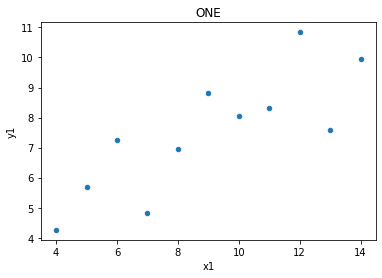
# plot the four datasets

one.plot(kind = 'scatter', x = 'x1', y = 'y1', title = 'ONE');
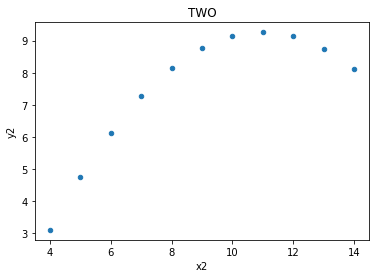
two.plot(kind = 'scatter', x = 'x2', y = 'y2', title = 'TWO');
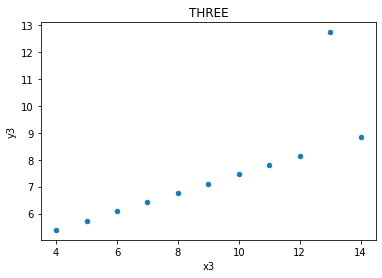
three.plot(kind = 'scatter', x = 'x3', y = 'y3', title = 'THREE');
four.plot(kind = 'scatter', x = 'x4', y = 'y4', title = 'FOUR');
_images/viz_summary_stats_8_0.png _images/viz_summary_stats_8_1.png _images/viz_summary_stats_8_2.png _images/viz_summary_stats_8_3.png

Lines

The relationships between x values and y values are similar when seen in lines, but of course are not the same, as the data is not the same (just the measures of central tendancy)

# define the two sets of data

x = np.array(one.x1)
y = np.array(one.y1)
plt.plot(x, y, 'o')

# establish the slope (m) and the intercept (c)

m, c = np.polyfit (x, y, 1)

# plot the linear regression

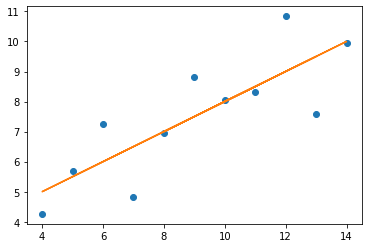
plt.plot (x, m * x + c)

# print the value of the slope and where it's situated (in terms of the y-axis)

print('slope:', m.round(5), 'y-int:', c.round(5))

slope: 0.50009 y-int: 3.00009
_images/viz_summary_stats_10_1.png 
x = np.array(two.x2)
y = np.array(two.y2)
plt.plot(x, y, 'o')

m, c = np.polyfit (x, y, 1)

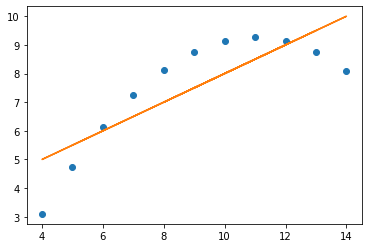
plt.plot (x, m * x + c)

print('slope:', m.round(5), 'y-int:', c.round(5))

slope: 0.5 y-int: 3.00091
_images/viz_summary_stats_11_1.png 
x = np.array(three.x3)
y = np.array(three.y3)
plt.plot(x, y, 'o')

m, c = np.polyfit (x, y, 1)

plt.plot (x, m * x + c)

print('slope:', m.round(5), 'y-int:', c.round(5))

slope: 0.49973 y-int: 3.00245
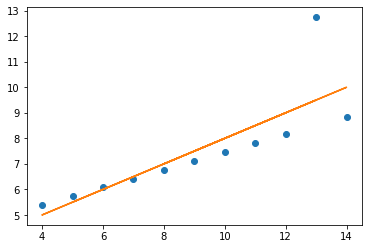
_images/viz_summary_stats_12_1.png 
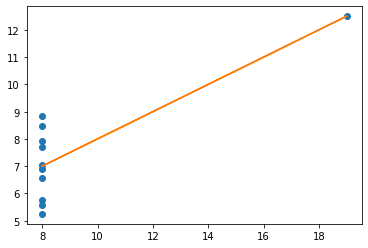
x = np.array(four.x4)
y = np.array(four.y4)
plt.plot(x, y, 'o')

m, c = np.polyfit (x, y, 1)

plt.plot (x, m * x + c)

print('slope:', m.round(5), 'y-int:', c.round(5))

slope: 0.49991 y-int: 3.00173
_images/viz_summary_stats_13_1.png

Datasaurus (2016)

path = '/Users/aidanair/Documents/DATA/ALL_DATASETS/'
file = 'datasaurus_data.csv'

cols = ['town_A', 'town_B']
din = pd.read_csv(path + file, names = cols)

# say the data refers to two towns...

din
town_A town_B
0 55.3846 97.1795
1 51.5385 96.0256
2 46.1538 94.4872
3 42.8205 91.4103
4 40.7692 88.3333
... ... ...
137 39.4872 25.3846
138 91.2821 41.5385
139 50.0000 95.7692
140 47.9487 95.0000
141 44.1026 92.6923

142 rows × 2 columns

# scatter plot to show any trends in the relationship betwen the data in town A, and the data in town B

din.plot.scatter(x = 'town_A', y = 'town_B');
_images/viz_summary_stats_17_0.png

Datasaurus dozen (2017)

path = '/Users/aidanair/Documents/DATA/ALL_DATASETS/'
file1 = 'DatasaurusDozen.tsv'

d = pd.read_csv(path + file1, sep = "\t")

print(d.shape)
d[:3]

(1846, 3)
dataset x y
0 dino 55.3846 97.1795
1 dino 51.5385 96.0256
2 dino 46.1538 94.4872

“These 13 datasets (the Datasaurus, plus 12 others) each have the same summary statistics (x/y mean, x/y standard deviation, and Pearson’s correlation) to two decimal places, while being drastically different in appearance.”

## Consider two of the dozen

display_side_by_side(d[d.dataset == 'away'].head(), 
                     d[d.dataset == 'bullseye'].head(), 
                     titles=['away','bullseye'])

away

dataset x y
142 away 32.331110 61.411101
143 away 53.421463 26.186880
144 away 63.920202 30.832194
145 away 70.289506 82.533649
146 away 34.118830 45.734551

bullseye

dataset x y
1278 bullseye 51.203891 83.339777
1279 bullseye 58.974470 85.499818
1280 bullseye 51.872073 85.829738
1281 bullseye 48.179931 85.045117
1282 bullseye 41.683200 84.017941 
# Show the correlation measure, and the mean and std for x values and y values in each of the two datasets

print('(Pearson) Correlation between x and y values for "Away" and "Bullseye" datasets')
print('Away:', np.corrcoef(d[d.dataset == 'away'].x, d[d.dataset == 'away'].y)[1][0].round(3))
print('Bullseye:', np.corrcoef(d[d.dataset == 'bullseye'].x, d[d.dataset == 'bullseye'].y)[1][0].round(3))

display_side_by_side(d[d.dataset == 'away'].describe().round(2), 
                     d[d.dataset == 'bullseye'].describe().round(2), 
                     titles=['away','bullseye'])

(Pearson) Correlation between x and y values for "Away" and "Bullseye" datasets
Away: -0.064
Bullseye: -0.069

away

x y
count 142.00 142.00
mean 54.27 47.83
std 16.77 26.94
min 15.56 0.02
25% 39.72 24.63
50% 53.34 47.54
75% 69.15 71.80
max 91.64 97.48

bullseye

x y
count 142.00 142.00
mean 54.27 47.83
std 16.77 26.94
min 19.29 9.69
25% 41.63 26.24
50% 53.84 47.38
75% 64.80 72.53
max 91.74 85.88 
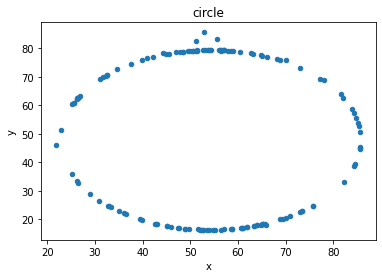
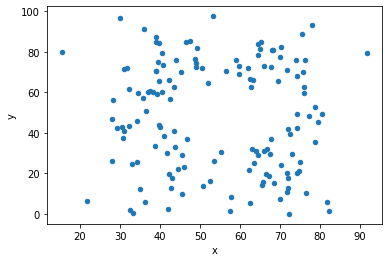
# plot both datasets, with their (almost) identical mean, std and correlation

df = d[d.dataset == 'away']
df.plot(kind = 'scatter', x = 'x', y = 'y');

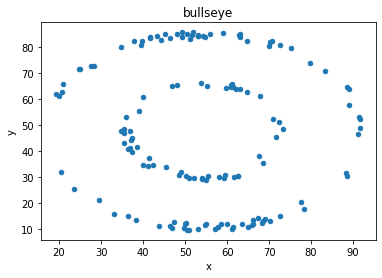
df = d[d.dataset == 'bullseye']
df.plot(kind = 'scatter', x = 'x', y = 'y');
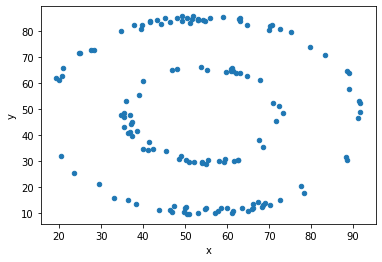
_images/viz_summary_stats_24_0.png _images/viz_summary_stats_24_1.png 
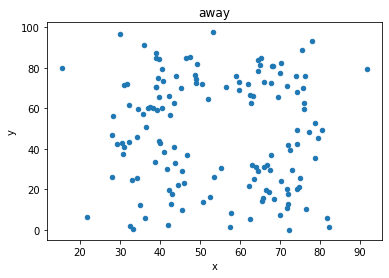
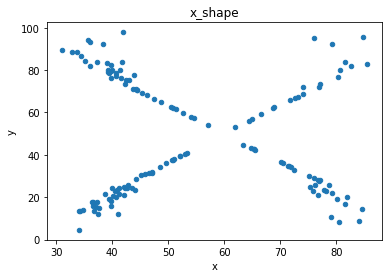
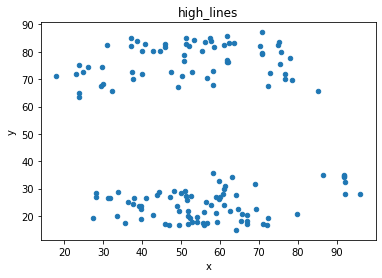
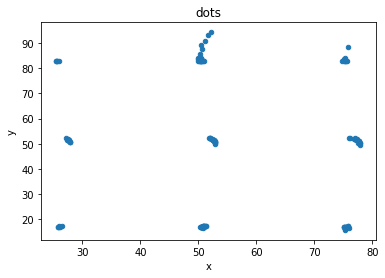
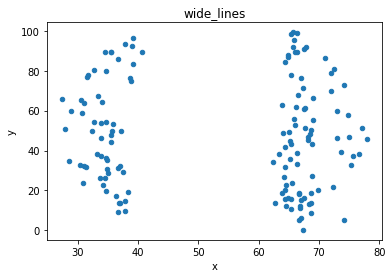
# plot the dinosaur and the dozen others

sets = d.dataset.unique().tolist()

for x in sets:
    df = d[d.dataset == x]
    df.plot(kind = 'scatter', x = 'x', y = 'y', title = x)
_images/viz_summary_stats_25_0.png _images/viz_summary_stats_25_1.png _images/viz_summary_stats_25_2.png _images/viz_summary_stats_25_3.png _images/viz_summary_stats_25_4.png _images/viz_summary_stats_25_5.png _images/viz_summary_stats_25_6.png _images/viz_summary_stats_25_7.png _images/viz_summary_stats_25_8.png _images/viz_summary_stats_25_9.png _images/viz_summary_stats_25_10.png _images/viz_summary_stats_25_11.png _images/viz_summary_stats_25_12.png
Basic charts in pandas Tools